Die vier Quantenzahlen beschreiben Elektronenzustände verschiedener Energie und Geometrie. Mit den vier Quantenzahlen lässt sich der Zustand eines Elektrons in Bezug auf den Atomkern eindeutig formulieren. Setzt man die vier Quantenzahlen in die Wellengleichung von Schrödinger ein, so erhält man eine Wellenfunktion, die sich von einem Punkt im Raum zu einem anderen ändert. Das Quadrat der Wellenfunktion entspricht der Aufenthaltswahrscheinlichkeit des Elektrons. Zeichnet man diese Funktion, so erhält man unscharfe Wolken der Aufenthaltswahrscheinlichkeit (Orbitale) für die Elektronen um den Kern, die mitunter Knotenflächen bilden.

Obwohl sich der Name des Orbitalmodells von "Orbit"="Bahn" herleitet, gibt man es hier völlig auf, den Elektronen Bahnen zuzuordnen.

1. Die Orbitalgröße wird durch die Hauptquantenzahl n ausgedrückt.
   Die Hauptquantenzahl kennzeichnet die Energiestufen n = 1-7 des Elektrons. Sie entspricht einer bestimmten "Bahn" nach dem Modell von Bohr (Elektronenschalen K, L, M, ...). Die maximale Elektronenzahl auf einer Energiestufe beträgt 2n². Wir werden aber später sehen, dass die Elektronen nicht um den Kern rotieren!
   
   
2. Die Orbitalform wird durch die Nebenquantenzahl l ausgedrückt.
   Die Nebenquantenzahl gibt die Raumorientierung energiegleicher Niveaus an. Jeder Hauptquantelzahl lassen sich Nebenquantenzahlen zuordnen. Man könnte nach Bohr die Nebenquantenzahlen als "Unterschalen" interpretieren. Die Nebenquantenzahlen können Werte von 0 bis n-1 annehmen.
   
   
3. Die Orientierung des Orbitals im Raum wird durch die Magnetquantenzahl m ausgedrückt.
   beschreibt, wie die Elektronenbahn im Raum relativ zu einem externen Standard, z.B. einem Magnetfeld oder einem elektrischen Feld, orientiert ist. Im Magnetfeld werden bestimmte Energieniveaus weiter aufgespalten. Die Magnetquantenzahl m kann die Werte - l ... 0 ... + l annehmen.
   
   
4. Die Spinquantenzahl s gibt den Drehsinn eines Elektrons an.
   Der  Spin eines Elektrons kann nur zwei verschiedene Werte haben:  +1/2 oder -1/2 .

Dabei ist folgendes zu beachten:

 

 

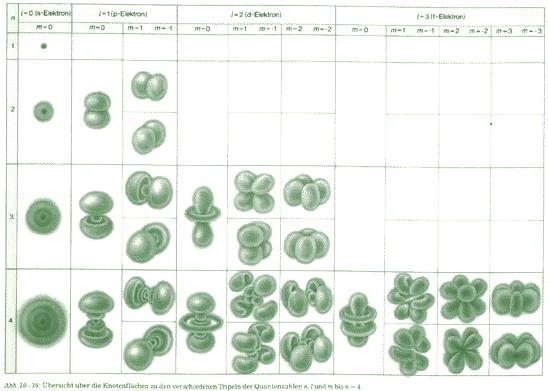
Die folgende Abbildung zeigt einige grafische Lösungen der Wellenfunktion:

• Bildquelle: Mike Friedrich und Daniel Schmidt, Berühmte Physiker, Erwin Schrödinger; am 1.8.12 abgerufen